中心極限定理をPythonで視覚的に理解する

Python

数学の世界には中心極限定理という必殺技のような定理が存在します。中心極限ってなんかかっこいいw

数学の定理を文字や式で眺めても、なかなかイメージできないこともあると思います。私自身も、学生の頃は教科書を眺めてもよく理解できず困りました。

ところがPythonを使えば、実際に計算したり図示したりしてその定理を試すことができるのです。実際の結果を見たらへぇ～と納得できることもあると思います。

そこで今回は、中心極限定理をPythonで試してみようと思います。グラフを描いて確認していくので、きっと皆さんも理解していただけると思います^^

目次

中心極限定理とは

端的に中心極限定理を説明すると、「母集団がどのような分布をしていても、そこから取り出した標本の平均値の分布は、平均を計算する回数が大きくなるにつれて正規分布に近づく」ということになります。

数学チックに書くと、平均μ、分散σ2のあらゆる分布から無作為抽出した標本の標本平均Xの分布は、（無作為抽出した）nが大きくなるにつれ平均μ、分散σ2/nの正規分布N(μ, σ2/n)に近づく。

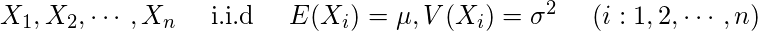
X_1,X_2,\cdots ,X_n \hspace{5mm} \mbox{i.i.d} \hspace{5mm} E(X_i)=\mu , V(X_i)=\sigma^2 \hspace{5mm} (i:1,2,\cdots,n)
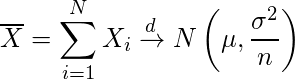
\overline{X}=\displaystyle \sum_{i=1}^{N}{X_i} \xrightarrow{d} N \left( \mu,\displaystyle\frac{\sigma^2}{n} \right)

この辺りは一部の天才にしか理解できません。気にせず退散しましょう。

そもそも、いかなる分布でも~~~正規分布に従うという文言、直感に反している感じがしませんか？ということで実際にそうなるのかをPythonで試してみようと思います。

正規分布以外の様々な分布の標本平均をプロットし、nが大きくなるほど正規分布に近づくのか確かめます。

Pythonで実装

Pythonで確かめるために、numpyとmatplotlibを使います。

import numpy as np
import matplotlib.pyplot as plt

一様分布

一様分布とは？

一様分布とは、確率密度関数がどの範囲でも一定の分布を指します。

最もわかりやすい例の1つとして、さいころの出る目があります。普通のさいころであれば、どの目が出る確率も1/6になります。さいころを何度も振ったときの出た目の分布は一様分布となります。

n=100のとき

一様分布の母集団から抽出した100個の標本の平均を算出する作業を100回繰り返し、その結果をヒストグラムにします。

mean_list = []
#100回試行
for i in range(100):
    arr = np.random.random_sample(100)
    mean = arr.mean()
    mean_list.append(mean)
plt.hist(mean_list, range=[0.46, 0.57], bins=100)
plt.hist(mean_list, range=[0.46, 0.57], bins=100)

ヒストグラムを見るに、正規分布という感じではなさそうです。

n=1000のとき

続いて、標本平均を1000回算出してプロットしてみます。

mean_list2 = []
#1000回試行
for i in range(1000):
    arr = np.random.random_sample(100)
    mean = arr.mean()
    mean_list2.append(mean)
plt.hist(mean_list2, range=[0.46, 0.57], bins=100)
plt.hist(mean_list2, bins=100)

n=100の場合よりも正規分布に近づいた形になっていることがわかります。

n=10000のとき

さらに標本数を増やして実行してみます。

mean_list3 = []
#10000回試行
for i in range(10000):
    arr = np.random.random_sample(100)
    mean = arr.mean()
    mean_list3.append(mean)
plt.hist(mean_list3, range=[0.46, 0.57], bins=100)
plt.hist(mean_list3, bins=100)

このように、一様分布において中止極限定理が言わんとしていることは正しそうであることがわかりました。

二項分布

続いて二項分布で中心極限定理を検証してみます。

二項分布とは？

二項分布の前提として「ベルヌーイ試行」について知っておく必要があります。ベルヌーイ試行とは、起こる結果が2つしかない試行のことを指します。「コインを投げて表が出るか裏が出るか」といったようなものがベルヌーイ試行です。

このベルヌーイ試行をn回行ったとき、成功する回数Xが従う確率分布を「二項分布」と言います。

n=100のとき

二項分布の母集団から抽出した100個の標本の平均を算出する作業を100回繰り返し、その結果をヒストグラムにします。

mean_list = []
for i in range(100):
    arr = np.random.binomial(10, 0.5, 100)
    mean = arr.mean()
    mean_list.append(mean)
plt.hist(mean_list, range=[4, 6], bins=100)
plt.hist(mean_list, range=[4, 6], bins=100)

これが基準になります。

n=1000のとき

続いてn=1000の場合です。コードはほとんど同じなので割愛します。結果は以下のようになりました。

plt.hist(mean_list2, range=[4, 6], bins=100)

より山型になってきました。

n=10000のとき

さらに標本数を増やしてみます。

plt.hist(mean_list3, range=[4, 6], bins=100)

ヒストグラムのbinsが100と細かいため、崩れたようにも見えますが、グラフの粒度を荒くするとよりきれいな山型であることがわかります。

plt.hist(mean_list3, range=[4, 6], bins=50)
bins=50

カイ二乗分布

最後にカイ二乗分布で中心極限定理を検証してみます。

カイ二乗分布とは

カイ二乗分布は複数の独立した標準正規分布によって成り立ちます。

確率変数Z1,Z2, …,Zkが互いに独立であり、それぞれが標準正規分布N(0,1)に以下の式から算出される自由度kのχ2が従う確率分布を指します。

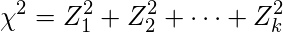
\displaystyle \chi^{2}=Z_{1}^{2}+Z_{2}^{2}+\cdots+Z_{k}^{2}

統計分野で、カイ二乗分布は母分散の区間推定や独立性の検定に用いられます。

n=100のとき

まずは100回試行したときのグラフです。

mean_list = []
#100回試行
for i in range(100):
    arr = arr = np.random.chisquare(10,100)
    mean = arr.mean()
    mean_list.append(mean)
plt.hist(mean_list, range=[9, 11], bins=100)
plt.hist(mean_list, range=[9, 11], bins=100)

ここから試行数を増やしていきます。

n=1000のとき

plt.hist(mean_list2, range=[9, 11], bins=100)

n=100のときよりもきれいな山型になってきました。

n=10000のとき

さらに試行数を増やしていきます。

plt.hist(mean_list3, range=[9, 11], bins=100)

かなり正規分布に近づいた気がします。

確かに、カイ二乗分布でも中心極限定理が該当するであろうことがわかりました。

Pythonでデータサイエンスするなら

Pythonでデータサイエンスをするなら、以下の書籍がおすすめです。Pandas、matplotlib、Numpy、scikit-learnといったデータサイエンスに必要なライブラリを、体系立てて一通り学ぶことができます。

ややお値段高めですが、これ1冊で十分という内容・ボリュームなので、損はしないと思います^^

まとめ

Pythonでグラフを描いて、中心極限定理を検証してみました。一様分布、二項分布、カイ二乗分布と、もとの分布の形は違えども、その標本平均のプロットは試行数が増えるにつれて正規分布に近づくことがわかりました。

数学で直感的に理解できないようなことも実際に検証できるのがPythonの強みでもあります。わからないことがあったら試してみるのが理解への近道かもしれませんね。

ではでは👋

Pythonの最新記事8件