【統計】t検定の原理と流れを理解する

統計

統計のメインディッシュといえば「検定」です。多くの人は、検定を使いこなすために統計を学んでいると言っても過言ではないのでしょう。

今回は2つの集団の母平均の差の検定について取り上げます。2つの母集団からそれぞれ抽出した標本の平均に差があるかを検定することを「2標本t検定」といいます。科学論文では実験結果の統計解析はほぼ必須で、このt検定も非常によく使われます。

前回はt分布について取り上げましたが、t検定ではこのt分布を使って検定をします。

https://www.learning-nao.com/?p=2578

早速、t検定の流れを見ていきましょう。

目次

対応ありと対応なし

t検定は比較する集団のデータが互いに対応しているか、対応していないかによって検定統計量（集団に差があるかないかを判定する数値）の求め方が異なります。

対応なし2標本t検定

比較する2つの母集団に対応がない場合を考えます。全く異なる対象からそれぞれ抽出した2つの標本は「対応のないデータ」となります。

例えば肥満の人の集団と痩せた人の集団の体重の平均を比較したい場合、肥満の人の集団と痩せた人の集団にはそれぞれ別の人が属しているので、「対応の無いデータ」となります。このとき、両集団（群）は独立であると言えます。

対応の無いデータ例

実際の場面においても、対応なし2標本t検定を行う場面が多いのではないかと思います。

対応あり2標本t検定

同一の集団から抽出した対となる標本は「対応のあるデータ」となります。

例えばもともと肥満の集団に断食を1カ月課し、痩せさせたとします。断食前後での平均体重を比較したいとき、2つの集団の被験者は同一です。こういった場合が対応ありです。

対応のあるデータ例

対応あり2標本t検定は投薬実験などでよく用いられます（同じ被験者に対し投薬の前後で比較したい場合が多いので）。

また、対応あり2標本t検定の方が一般に検出力が高いです。検出力が高いとは、平均の差が同等であった場合、対応なしよりも対応ありの方が有意差が出やすいということです。同じ集団で平均値に変化があった場合の方が「違いがある」と判断しやすそうなのは、直感的にも理解できると思います。

前提条件

t検定が使える（検定統計量の分布がt分布になる）条件として、以下の2点を満たしている必要があります。

  • 母集団が正規分布に従う
  • 母集団の分散が等しい

この条件を満たした状態で行うt検定を「Studentのt検定」と言います。

これらを満たしていない場合、検定の種類を変える必要があります。というか、検定に使う2つの母集団の分散は普通未知の値です。なので、等しいと仮定して検定を行う場合が多いです。

帰無仮説

t検定における帰無仮説は「それぞれの集団の母平均は等しい」です。

検定統計量を求める

ということでt検定における検定統計量を求めてみます。今回は実際によくあるケースを想定して、対応なしの場合の検定統計量を求めます。

対応なしのt検定では、それぞれの標本が対応していないことを加味して統計量を求める必要があります。統計量tは次の式で求められます。

\displaystyle t=\frac{\overline{x}_{1}-\overline{x}_{2}-(\mu_1-\mu_2)}{\sqrt{s^{2}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}}

このとき、1群目の標本平均が、母平均が、サンプリングがです。2群目の標本平均が、母平均が、サンプルサイズがです。

帰無仮説「それぞれの集団の母平均は等しい」より、–=0が成り立ちます。よって、

\displaystyle t=\frac{\overline{x}_{1}-\overline{x}_{2}}{\sqrt{s^{2}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}}

となります。

プールした分散s2

s2は不偏分散ですが、2つの集団の標本から算出した「プールした分散s2」を求める必要があります。プールした分散とは、となります。したがって、全データにおける平均からの偏差の2乗和を全体の自由度で割ったものです。

今回、母集団の分散は等しいという仮定の下で検定を進めています。なので、それらを足し合わせた全ての標本から分散を算出します。手順としては、全データ（n1+n2）における平均からの偏差の2乗和を、全体の自由度で割ります。

全データ（n1+n2）における平均からの偏差の2乗和

とを足し合わせたものがこれに相当します。

さて、不偏分散を求める式はでした。これを式変換すると、

\sum_{i = 1}^n {(x_i - \overline{x})^2} = (n - 1)s^2
不偏分散の式変換した形

となります。したがって、全データにおける平均からの偏差の2乗和は

(n_1-1){{s'}_1}^2+(n_2-1){{s'}_2}^2

となります。

全体の自由度

続いて自由度を求めます。不偏分散を求める際の自由度は「n-1」でした（上記の不偏分散の式参照）。プールした分散を求める際も不偏分散を用いているので自由度は「n-1でいいのでしょうか？」

答えはNoです。

プールした分散を求める際には、2つの集団からの標本を足し合わせて計算しています。このとき、集団Aの自由度は「n1-1」、集団Bの自由度は「n2-1」です。全体の自由度はこれらの自由度を足し合わせた値になります。したがって、「n1＋n2-2」が全体の自由度です。

ここまで求まれば、プールした分散を求めることができます。プールした分散s2は以下の式で求められます。

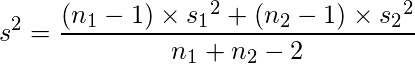
\displaystyle s^{2}=\frac{(n_{1}-1) \times {s_{1}}^{2}+(n_{2}-1) \times {s_{2}}^{2}}{n_{1}+n_{2}-2}
プールした分散

この値を上記のtを求める式に代入すると、検定統計量が求まります。

このように2つの標本を１つにまとめることによって、推定精度を高めることができます。

検定統計量の評価

検定統計量tが求まったところで、帰無仮説「それぞれの集団の母平均は等しい」が棄却できるかできないかを評価する必要があります。

評価にはt分布表を用います。縦軸は、自由度、横軸は有意水準です。

t分布表

例えば、全体の自由度10で有意水準5%の片側検定を考えます。この場合、縦軸10、横軸0.05で交差する値が基準となるt値です。今回は1.182です。

評価は算出したt値が基準となるt値を超えているかどうかで行います。片側検定の場合は基準値より求めたt値が大きければ帰無仮説は棄却され、対立仮説が採択されます。

例えば検定で求めたt値が1.10の場合は帰無仮説は棄却されません。逆に、t値が2.00だった場合は帰無仮説が棄却されます。

統計学を学ぶなら

以下は統計学のとっかかりには最適の一冊です。説明が丁寧なうえ難しい数式は使わず、原理を説明してくれています。

慣れてくれば、以下がオススメです。統計学の基礎、用語をしっかりと押さえることができます。とっかかりにはやや難しい書籍ですが、ある程度数式にも慣れてきた方はぜひ。

まとめ

t検定について、t検定の流れとその原理を見ていきました。

2標本での検定ではこのt検定が非常によく使われます。また、t検定の中にも条件によって様々な種類があり、奥が深いです。

多くの場合計算式まで理解しておく必要はないと思います。少なくとも大まかな計算の流れと結果の見方を把握しておけば、現場でも検定が使えるようになるのではないでしょうか！

次回はPythonでt検定をやってみます。

【統計】Pythonでt検定をやってみる

ではでは👋

統計の最新記事8件